Ligand and Crystal Field theories are used to describe the nature of the bonding in transition metal complexes. Crystal Field Theory is based upon the effect of a perturbation of the d-orbitals consisting of electronic interaction between the metal cation nucleus and the negatively charged electrons of the ligands: the metal-ligand interactions are electrostatic only. Ligand Field Theory treats the metal-ligand interaction as a covalent bonding interaction, and depends upon considering the overlap between the d-orbitals on the metals and the ligand donor orbitals.
Crystal Field Theory
Let us consider an octahedral arrangement of ligands around the central metal ion. For the octahedral field generated, the ligands are considered to be point charges sited on the cartesian axes, and the effect these point charges have on the valence orbitals of the metal ion is calculated.
The s-orbital of the metal is spherically symmetric, and so the result of its interaction with the ligand field is that its energy is raised: the increased repulsion between the negative point charges representing the ligands and the negative charge of the electrons in the s-orbital mean that the s-orbital electrons lie at higher energy.
Similarly, the metal p-orbitals lie along the cartesian axes, and so point directly towards the point charges, and this means that the p-orbitals all have the same degree of interaction with the ligands, and so they remain degenerate, but the extra repulsion between the p-orbital electrons and the point charges of the ligands means that the p-orbitals are raised in energy.
| Crystal field around the metal s-orbital | Crystal Field around the metal p-orbitals |
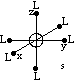 |
 |
The main effect the introduction of the ligands has on the orbitals of the metal ion is on the d-orbitals. The symmetry of the d-orbitals means that they fall into two categories when the ligand field is introduced. Some of the orbitals point directly towards the ligands, and some point between the ligands.
|
||||||
| d-orbitals which point between the ligands | ||||||
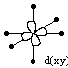 |
 |
 |
||||
The d(x2-y2) and d(z2) orbitals have lobes which point directly towards the point charges of the ligands, and so the have a greater electrostatic repulsion. The d(xy), d(xz), and d(yz) orbitals have lobes which point between the charges, and so have a lesser electrostatic repulsion.
Therefore, the d-orbitals are no longer degenerate, due to their different electrostatic repulsion with the ligands, and they split into two groups which have different energies. Group theory can be used to show that the d(x2-y2) and d(z2) orbitals belong to the eg symmetry group in the octahedral field, and the d(xy), d(xz), and d(yz) orbitals belong to the t2g symmetry group.
|
Orbital diagram for the metal orbitals in the octahedral Crystal Field |
|
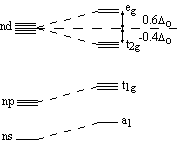 |
The metal s- and p-orbitals increase in energy, and the d-orbitals split into two groups in the octahedral field. The difference in energy between the two sets is the ligand field splitting parameter, Δo. |
The energy difference between the two sets of orbitals from the d-orbitals in the crystal field is known as the ligand field splitting parameter, Δo, where the o refers to the fact that it is an octahedral field. Conservation of energy states that the energies of the t2g orbitals lie at -0.4Δo and the eg orbitals lie at +0.6Δo, so the total energy is [3x(-0.4Δo)]+[2x(+0.6Δo)] = 0.

